一文读懂RateLimiter原理与细节 - Google Guava RateLimiter

一文读懂RateLimiter原理与细节 - Google Guava RateLimiter ^置顶！

2022-05-26/2023-03-16 | 0 评论 | 2,302 浏览

SmoothBursty RateLimitor

/**
 * 对外暴露的创建方法
 */
public static RateLimiter create(double permitsPerSecond) {
    /*
     *  内部调用一个qps设定 + 起始时间stopwatch的构建函数.
     */
    return create(permitsPerSecond, SleepingStopwatch.createFromSystemTimer());
  }

这里传入的SleepingStopwatch是一个以系统启动时间的一个相对时间的计量. 后面的读时间偏移又是以这个开始的时间偏移为起始.
接着展开上面里面的create函数:

@VisibleForTesting
  static RateLimiter create(double permitsPerSecond, SleepingStopwatch stopwatch) {
   // 这里的构造什么都没有做.
    RateLimiter rateLimiter = new SmoothBursty(stopwatch, 1.0 /* maxBurstSeconds */);
    rateLimiter.setRate(permitsPerSecond);
    return rateLimiter;
  }

构建函数就是初始化两个参数.无它 , 重点在下面的setRate 函数.

SmoothBursty(SleepingStopwatch stopwatch, double maxBurstSeconds) {
      super(stopwatch);
      this.maxBurstSeconds = maxBurstSeconds;
    }

setRate

public final void setRate(double permitsPerSecond) {
    checkArgument(
        permitsPerSecond > 0.0 && !Double.isNaN(permitsPerSecond), "rate must be positive");
   // 在同步代码块中进行比率设定.
    synchronized (mutex()) {
      doSetRate(permitsPerSecond, stopwatch.readMicros());
    }
  }

doSetRate

// 这是一个可以重复调用的函数.第一次调用和非第一次调用的过程有些不一样.
// 目的是设定一个新的Rate率.
@Override
  final void doSetRate(double permitsPerSecond, long nowMicros) {
   // 重试计算和同步存储的预分配的令牌.
    resync(nowMicros);
   // 计算稳定的发令牌的时间间隔. 单位us , 比如qps为5, 则为 200ms即 20万us的间隔进行令牌发放. 
    double stableIntervalMicros = SECONDS.toMicros(1L) / permitsPerSecond;
    this.stableIntervalMicros = stableIntervalMicros;
    // 调用内部的 比率设定.
    doSetRate(permitsPerSecond, stableIntervalMicros);
  }

注意: 第一次调用这个函数的时候.得到的结果是.没有预存储的值. 下一个可以计算令牌的起始时间"同步"到与开始传入的时间偏移一致.
总之,就是一个 initial state

// 注: 第一次在构建的时候的调用的话. 
// coolDownIntervalMicros = 0
// nextFreeTicketMicros = 0
// newPermits = 无穷大.
// maxPermits = 0 (初始值,还没有重新计算)
// 最后得到的: storedPermits = 0;
// 同时: nextFreeTicketMicros = "起始时间"
void resync(long nowMicros) {
    // if nextFreeTicket is in the past, resync to now
    if (nowMicros > nextFreeTicketMicros) {
      double newPermits = (nowMicros - nextFreeTicketMicros) / coolDownIntervalMicros();
      storedPermits = min(maxPermits, storedPermits + newPermits);
      nextFreeTicketMicros = nowMicros;
    }
  }

下面的doSetRate是一个接口. 由不同实现类实现.

// SmoothBursty RateLimitor 的实现.
@Override
    void doSetRate(double permitsPerSecond, double stableIntervalMicros) {
      // 初次设定的时候,oldMaxPermits  = 0.0
      double oldMaxPermits = this.maxPermits;
     // 新的(当前的) maxPermits 为 burst的时间周期(1秒) * 每周期的令牌数. (xxx qps)
      maxPermits = maxBurstSeconds * permitsPerSecond;
      if (oldMaxPermits == Double.POSITIVE_INFINITY) {
        // if we don't special-case this, we would get storedPermits == NaN, below
        storedPermits = maxPermits;
      } else {
       // 初始走这里. storedPermits 仍然初始初始化为 0.0
        storedPermits =
            (oldMaxPermits == 0.0)
                ? 0.0 // initial state
                : storedPermits * maxPermits / oldMaxPermits;
      }
    }

简单总结一下:
在构建完成我们想要的 SmoothBursty RateLimitor 后, 我们的limitor的初始状态如下:

maxBurstSeconds 为1 (秒)

storedPermits (为0 , 没有预分配的令牌.处于一个初始的状态)

stableIntervalMicros, 间隔为设定为我们的qps所换算的每一个令牌发放时的时间间隔.单位 us

maxPermits: 最大允许个数为突发周期*每周期信息数. 这里突发周期为限定死了为一秒. 也就是可以预存储一个周期的令牌.

nextFreeTicketMicros: 下一次可以发放令牌计时的起始时间. 初始化为 "开始偏移."

现在我们来看看怎么使用:

无限等待的获取.

@CanIgnoreReturnValue
  public double acquire(int permits) {
    // 保留,预定这么多的令牌数, 返回需要等待的时间.
    long microsToWait = reserve(permits);
   // 把需要等待的时间补齐, 这样以满足限流的需求.
    stopwatch.sleepMicrosUninterruptibly(microsToWait);
    // 返回给调用者,这次调用用了多少时间.
    return 1.0 * microsToWait / SECONDS.toMicros(1L);
  }

有超时时间的获取.

public boolean tryAcquire(int permits, long timeout, TimeUnit unit) {
    long timeoutMicros = max(unit.toMicros(timeout), 0);
    checkPermits(permits);
    long microsToWait;
    synchronized (mutex()) {
      long nowMicros = stopwatch.readMicros();
      if (!canAcquire(nowMicros, timeoutMicros)) {
        return false;
      } else {
        microsToWait = reserveAndGetWaitLength(permits, nowMicros);
      }
    }
    stopwatch.sleepMicrosUninterruptibly(microsToWait);
    return true;
  }

我们先看不设定超时时间的版本,这个比较简单. 核心是看里面的预定令牌的需要的时间的计算.

final long reserve(int permits) {
    checkPermits(permits);
    synchronized (mutex()) {
      return reserveAndGetWaitLength(permits, stopwatch.readMicros());
    }
  }

再往里面:

/**
   * Reserves next ticket and returns the wait time that the caller must wait for.
   *  预定下一个ticket ,并且返回需要等待的时间.
   * @return the required wait time, never negative
   */
  final long reserveAndGetWaitLength(int permits, long nowMicros) {
    long momentAvailable = reserveEarliestAvailable(permits, nowMicros);
    return max(momentAvailable - nowMicros, 0);
  }

reserveEarliestAvailable 实现

@Override
  final long reserveEarliestAvailable(int requiredPermits, long nowMicros) {
    // 此时调用这个就与之前初始化的时候不一样.
    // 会把"没有过期"的存储起来. 但是如果计数时间是在未来. 那就不做任何处理.
    resync(nowMicros);
    // 下次计数开始时间.
    long returnValue = nextFreeTicketMicros;
    // 存储的信息可供(需要)消费的量
    double storedPermitsToSpend = min(requiredPermits, this.storedPermits);
    // 需要等待的 新鲜permits
    double freshPermits = requiredPermits - storedPermitsToSpend;
    long waitMicros =
        storedPermitsToWaitTime(this.storedPermits, storedPermitsToSpend) // 对于SmoothBursty 来说 storedPermitsToWaitTime ,已经存储的令牌不需要等待.
            + (long) (freshPermits * stableIntervalMicros); // 新鲜的令牌需要等相应的时间间隔.
    // 由于可能的fresh令牌已经被预消费. 那我们的令牌计数时间就得往后移.以表示这段时间被预消费了.
    this.nextFreeTicketMicros = LongMath.saturatedAdd(nextFreeTicketMicros, waitMicros);
    // 最后一步把上面计算的可扣减的量从存储的量里面减掉.
    this.storedPermits -= storedPermitsToSpend;
    // 返回我们需要等待的时间.
    return returnValue;
  }

  void resync(long nowMicros) {
    // if nextFreeTicket is in the past, resync to now
    // 一般当前的时间是大于计数起始时间的.
    //    此时: 把过去的时间换成令牌存储起来. 如果大于了最大的存储集数,就直接存上限. 这个是用于比如我系统初始化好后,刚开始没有流量.或者是一段时间没有流量后突然来了流量, 此时可以往"后"预存储一秒的时间的permits. 也就是我们常常说的burst的能力.
    // 如果计数开始时间.在未来的一个时间点. 那这个if不满足.不更新.
    // 此种发生在: 进行了"预借" 令牌的情况下.  
    if (nowMicros > nextFreeTicketMicros) {
      double newPermits = (nowMicros - nextFreeTicketMicros) / coolDownIntervalMicros();
      storedPermits = min(maxPermits, storedPermits + newPermits);
      nextFreeTicketMicros = nowMicros;
    }
  }

// 这是一个抽象函数. 对于 SmoothBursty 直接返回0 . 可以认为已经预分配的令牌,在获取时不需要待待时间.
abstract long storedPermitsToWaitTime(double storedPermits, double permitsToTake);

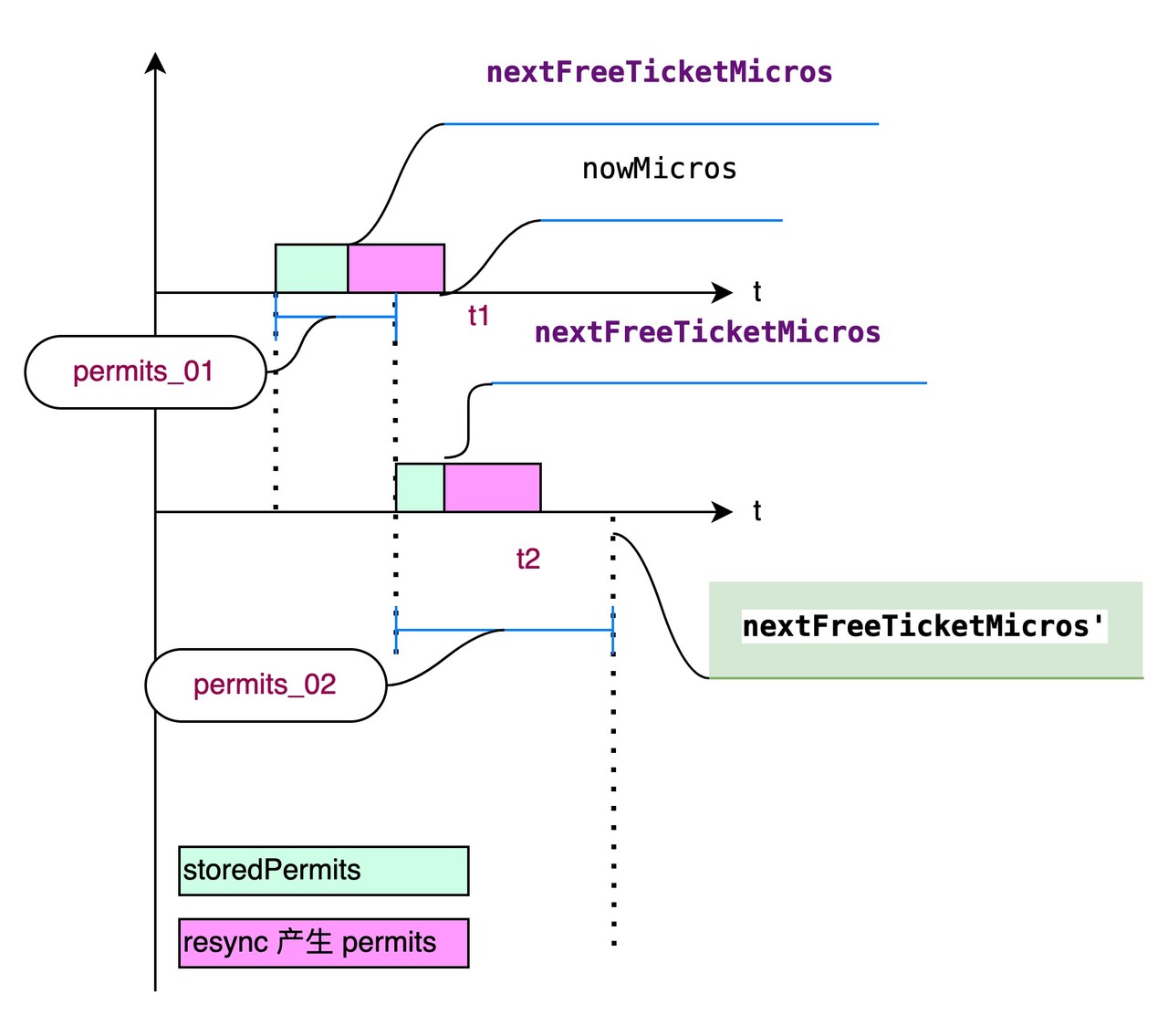
我们可以结合着上图来分析一下:

青色代表已经存储的令牌(permits)
紫色代表新同步时间产生的令牌(permits)
分析时间t1
- 在时刻t1请求一个令牌量:permits_01
- 此时青色中已经存储了部分令牌,但是不够
- 同步时间轴后, 产生了部分紫色的新令牌.
- 重新计算可用令牌: (青色与紫色加一起 ,但是如果和超过了一个burst周期,最一个周期的最大值MaxStoredPermits)
- 此时消费后,还剩余部分的存储量在t2时刻的图中表示为青色的那部分.
- 而此时nextFreeTicketMicros已经记为了:t1
分析时间t2
- 此时请求令牌量: pertmits_02
- 此时青色部分已经存储的令牌数不够.
- 同步时间轴后,产生了紫色部分的令牌量.
- 但是此时,已经产生的令牌量还是不够消费.
- 因此需要一个freshPermits的量度的时间间隔量.
- 然后: 令牌可计数开始时间:nextFreeTicketMicros被更新到t2时刻时的一个未来时间.此时产生了预支.
- 如果在这个可计数的时间点: nextFreeTicketMicros 到来之前,直接tryAcquire,但没有等待时间时,会直接失败.

总结

对于SmoothBursty类型的限流器来说,总是在某一个时间. 可以往前存储一分钟的burst流量的permits. (前提是没有被消费)

对于1的例外: ratelimiter初始的时刻,此时不会往前数. 实际计算实现的方式时, nowTime - nextFreeTicketMicros

对于一般场景: nextFreeTicketMicros是一个过去的值. 这样有差值就可以预存.

但是对于开始的时候, nextFreeTicketMicros会初始化为nowtime因此, 不存在burst.

但是对于开始的时候,或者是任意的其它时刻, 都可以往后借时间的token来消费.

但是对于借的令牌. 当前消费者是不承担的,由下一次消费的消费方来承担. 可以看上面的函数reserveEarliestAvailable中的处理.

当前函数不处理等待,那下一次请求的时候,是怎么处理的呢. 听起来好像也是不等待. ?

实际不是: 答案就在上面的resync 方法里. reserveEarliestAvailable 函数每次先会调用一次 resync函数. 得到新的nextFreeTicketMicros, 但是这个调用如果是在有欠债的时候.它是不做任何更新的. 然后这个reserveEarliestAvailable会返回一个resync后的时间点. 让当前的调用等到这个时间点.

再展开说就是: 如果没有欠时间, 那当前返回的时间就是now. 因此上面会调用sleep但是不会有任何的作用. 此时,不管当前存储的令牌是否够你用,你都不需要等待.

如果是nextFreeTicketMicros一个未来的时间, 那当前调用就等到这个未来的时间. 但是如果令牌在这个时间点还是不够,你可以预支后面的.这部分不需要你等待.

我可以用一个更直观的场景来描述一下这个问题:

当程序冷却了一段时间后. (已经完成了初始化.但是没有任何流量,持续了很长的时间.)
此时比如来了一个acquire(200) . 此时不管已经存储的有多少. (当然上一句描述的"一段时间"大于一秒的话.那就只能存储maxStoredPermits). 我都可以消费者这些已经存储的令牌. 并且在不够的时候我可以预支后面的令牌,并且不需要等待.
但是下一人过来就没有这么好运了. 他需要等待我预支的这么长的时间.比如每秒产生150个令牌. 那上面我是预支了 50个令牌. 此时这个人得把这产生50个令牌的时间等齐.但是他请求了额外的令牌.比如,他也是要了200个. 那他只等了50个令牌的时间.然后, 预支了150个令牌. 好像他比我幸运些.虽然等了50个.但是他可以预支150个. 只能说他还是走着去的.
但是第三个人来就没有这么好运了. 如果第三个人也要200个. 他得等待 150个令牌. 预支 50个令牌. 不管怎样.他还是能预支,这是事情好的一面

接下来我们再简单说说tryAcquire的实现逻辑.然后再把另外一个有预热的平滑限流器的逻辑补全.

我们再来看一下try的函数:

public boolean tryAcquire(int permits, long timeout, TimeUnit unit) {
    long timeoutMicros = max(unit.toMicros(timeout), 0);
    checkPermits(permits);
    long microsToWait;
    synchronized (mutex()) {
      long nowMicros = stopwatch.readMicros();
      // 特别注意的是这里. 这个判定逻辑.
      if (!canAcquire(nowMicros, timeoutMicros)) {
        return false;
      } else {
        microsToWait = reserveAndGetWaitLength(permits, nowMicros);
      }
    }
    stopwatch.sleepMicrosUninterruptibly(microsToWait);
    return true;
  }

我们看下上面注释中说明的要特别注意的地方的函数:canAcquire

private boolean canAcquire(long nowMicros, long timeoutMicros) {
    // 前一个函数:  queryEarliestAvailable 对于 smoothBursty来说就是nextFreeTicketMicros
    // 然后 换算一下:
    // nextFreeTicketMicros <= nowMicros + timeoutMicros
    // 也就是说,从当前这个时间,加一个可以等待的时间. 能够把将来时的  nextFreeTicketMicros 等成过去时, 那我们就可以等.
    // 换言之, 只要不是完成的预支我们就等.
    return queryEarliestAvailable(nowMicros) - timeoutMicros <= nowMicros;
  }

看上面的canAcquire 这个为什么返回false我们就不等了. 返回false为什么就不能等了呢? 原来啊. 像我们上面提到的, 我们的所有的获取令牌是可以透支的.

如果有预存的,我们可以使用一部分.如果不够可以预一部分. 但是不用等.
但是如果是纯预支. 那我们就得等相应的时间. 等完后. 至于我们要预支多少都是可以的. (预支的数由后人来还.就像中国的养老金一样)

同理,类比到这里. 如果等待一个时间后,还是纯预支,那我们相当于是在规定的时间内无法完成等待. 因此直接返回faslse. (按上面的原理,我们是在纯预支的时候要等足够的时间才能继续预支.否则要一直把时间等够.)

SmoothWarmingUp

public static RateLimiter create(double permitsPerSecond, long warmupPeriod, TimeUnit unit) {
    checkArgument(warmupPeriod >= 0, "warmupPeriod must not be negative: %s", warmupPeriod);
    return create(
        permitsPerSecond, warmupPeriod, unit, 3.0, SleepingStopwatch.createFromSystemTimer());
  }

  @VisibleForTesting
  static RateLimiter create(
      double permitsPerSecond,
      long warmupPeriod,
      TimeUnit unit,
      double coldFactor,
      SleepingStopwatch stopwatch) {
    RateLimiter rateLimiter = new SmoothWarmingUp(stopwatch, warmupPeriod, unit, coldFactor);
    rateLimiter.setRate(permitsPerSecond);
    return rateLimiter;
  }

    SmoothWarmingUp(
        SleepingStopwatch stopwatch, long warmupPeriod, TimeUnit timeUnit, double coldFactor) {
      super(stopwatch);
      this.warmupPeriodMicros = timeUnit.toMicros(warmupPeriod);
      this.coldFactor = coldFactor;
    }

从构造函数看,基本是一样的.流程. 只是在初始化的时候多了一个变量.: coldFactor
另外doSetRate不一样:

abstract void doSetRate(double permitsPerSecond, double stableIntervalMicros);

@Override
    void doSetRate(double permitsPerSecond, double stableIntervalMicros) {
      // 与上面一样.初始值是maxPermits: 0
      double oldMaxPermits = maxPermits;
      //  stableIntervalMicros 在这里的时候已经由上面的调用者设定为了有效值 1 / qps 
      //  coldFactor 默认会初始化为 3: 
      //  因此这个冷却时间coldIntervalMicros 的令牌间隔是 3倍于普通间隔
      double coldIntervalMicros = stableIntervalMicros * coldFactor;
      //  warmupPeriodMicros : 用户传入的预热时间.
      //  stableIntervalMicros:  稳定期间的令牌发生间隔.
      //  Permits的阈值(thresholdPermits)是:   0.5 * 预热时间期间正常能发的令牌量. 
      //  换言之,这预热一半的量.
      thresholdPermits = 0.5 * warmupPeriodMicros / stableIntervalMicros;
      // 
      maxPermits =
          thresholdPermits + 2.0 * warmupPeriodMicros / (stableIntervalMicros + coldIntervalMicros);
      slope = (coldIntervalMicros - stableIntervalMicros) / (maxPermits - thresholdPermits);
      if (oldMaxPermits == Double.POSITIVE_INFINITY) {
        // if we don't special-case this, we would get storedPermits == NaN, below
        storedPermits = 0.0;
      } else {
        storedPermits =
            (oldMaxPermits == 0.0)
                ? maxPermits // initial state is cold
                : storedPermits * maxPermits / oldMaxPermits;
      }
    }

我们看一下maxPermitts是怎么计算出来的.

maxPermits =
          thresholdPermits + 2.0 * warmupPeriodMicros / (stableIntervalMicros + coldIntervalMicros);

作一个变化:
maxPermits - thresholdPermits = 
       2* warmupPeriodMicros / (stableIntervalMicros + coldIntervalMicros)
继续:

(stableIntervalMicros + coldIntervalMicros) * (maxPermits - thresholdPermits ) / 2 = warmupPeriodMicros

我们再看一下这个图:

结合上面的公式:

(stableIntervalMicros + coldIntervalMicros) * (maxPermits - thresholdPermits ) / 2 = warmupPeriodMicros

maxPermits - thresholdPermits 实际就是梯形的高

stableIntervalMicros + coldIntervalMicros 这个是梯形的两个底.的和.

实际梯形面积公式就是:

面积(S) = (上底 + 下底) * 高 / 2

所以上面的maxPermit是怎么计算出来的就比较明确的. 先有一个梯形的面积代表warmup时间.( 每一个令牌发一个就有一个dt来代表需要的时间.把最大的permits发完时, 那它需要的总时间就是预热时间. 实际面积就是对这个绿色部分的积分 )

所以核心就是预热的时间总和是传入的预热时间. 而在预热期间能产生多少令牌,就是根据我们的冷却因子, 和稳定时的间隔. 以及这个预热周期的值 .就确定了最大的令牌是多少.我们拿一个示例讲下:

假如QPS: 100
预热时间为5秒.
那

stableIntervalMicros = 10ms
coldIntervalMicros = 10*3 = 30ms , (也就是说在预热期间,最慢会慢到到30ms产生一个令牌)
预热周期为: 5000 ms.

面积:(5000ms) = ( 上底(10ms) + 下底(30ms) ) * h / 2
那h = 10000 / 40 = 250 (个令牌)

前面的 0.5 * 预热周期(5000ms) / 稳定的间隔(10ms) = 250个.
这样就是把预热周期 5秒以内的平均要产生的 500个令牌. 前一半以正常的速率 10ms一个产生.
剩下的一半的令牌用可以生成原来两倍的令牌数的时间生成一半的令牌.

我们再看上上面的公式:

maxPermits =
thresholdPermits + 2.0 * warmupPeriodMicros / (stableIntervalMicros + coldIntervalMicros);

因为冷却的间隔是3倍.那间隔总体变为了4倍. 也就是原来的1/4 , 然后再乘以2. 因此后半部分:2.0 * warmupPeriodMicros / (stableIntervalMicros + coldIntervalMicros) 也是0.5倍* 预热周期 / 稳定间隔.

总结: 带有预热型的限流器. 会用一个预热周期的时间配合以稳定的间隔来确定一个最大可以存储的预支配的令牌数. 其中的一半, 是以稳定的正常速率产生的. 另外的一半的产生速率是"正常速率的一半"

再看一下拿已经产生的令牌的数据时需要消耗的时间:

这个时间在上面的突发流量型里面是为0的,也就是已经预生成的令牌是不需要再花额外的时间等待的.

@Override
    long storedPermitsToWaitTime(double storedPermits, double permitsToTake) {
      // 看看存储的令牌里面是否多于 阈值的 令牌
      // ******************这句代码要重点理解.  ****************
     //  我们存储的令牌数如果大于了阈值. 那就是说我们的系统冷却了. 需要一个预热的过程.    
     //  换句话说, 我们的代码要先从预热的逻辑走. 这部分的产生令牌的速率是依次变快的
     //. 因此在积分的时候,从右往往进行积分. 也就是说当足够冷却的时候. 进来的第一个请求是从3倍
    //  正常间隔开始的
      double availablePermitsAboveThreshold = storedPermits - thresholdPermits;
      long micros = 0;
      // measuring the integral on the right part of the function (the climbing line)
      // 测量 积分 在右边部分. (右边的攀岩线)
      if (availablePermitsAboveThreshold > 0.0) {
        // 存在需要积分计算的令牌. 取出高于阈值的需要积分的令牌数.
        double permitsAboveThresholdToTake = min(availablePermitsAboveThreshold, permitsToTake);
        // TODO(cpovirk): Figure out a good name for this variable.
        // 把需要的令牌数转换为时间.
        double length = permitsToTime(availablePermitsAboveThreshold)
                + permitsToTime(availablePermitsAboveThreshold - permitsAboveThresholdToTake);
        micros = (long) (permitsAboveThresholdToTake * length / 2.0);
        permitsToTake -= permitsAboveThresholdToTake;
      }

      // 测量(积分)左边的矩形部分. (如上图中的水平线的部分)
      // measuring the integral on the left part of the function (the horizontal line)     
      // 这个是计算左边矩形部分的面积, 如果上面存在右边梯形部分的token. 那上面的if
      // 正好会把右边的减掉. 此时剩余部分的就是矩形要计算的部分. 
      // 如果没有上面的if执行.那说明没有超过矩形的最长宽度. 因此也是直接计算. 
      micros += (long) (stableIntervalMicros * permitsToTake);
      return micros;
    }

    // 令牌数 转 时间
    private double permitsToTime(double permits) {
      // 基础稳定间隔时间. + 令牌数 * 斜率
      return stableIntervalMicros + permits * slope;
    }

RBA的技术分享